Neural Approaches to Robot Co-Optimization

Intelligent machines that sense or interact with their environment are comprised of both physical components for actuation and sensing, such as cameras, LiDARs, joints, limbs, and computational components, such as inference, perception, control, and planning algorithms. The design and configuration of physical components define an interface between software and the environment, providing both the input (sensors) and output (actuators) by which computational components make inferences about or control the world around them. Therefore, the success of inference or control is fundamentally linked to, and limited by, hardware design. Inference problems are easier when sensors measure data containing information about the quantity being inferred and control problems are easier when physical components allow for stable and efficient motions for the task at hand. Therefore, when designing intelligent systems, it is necessary to jointly consider the hardware of the system with its computational processes.

Traditionally, this design process has required multiple experts with extensive domain knowledge. For example, the process of creating a new gripper may involve one expert deciding on the type of gripper (e.g., pinch, suction, dexterous hand, etc.), the nature of the actuators (e.g., tendons vs. low-torque motors at the joints); and the type (e.g., vision or tactile) and placement of sensors. Given the resulting mechanical design, another expert will then be responsible for creating the inference and control algorithms that efficiently and robustly solve the distribution of manipulation problems relevant to the specific application. Such an approach has two fundamental limitations. First, this two-stage design process, which decouples the optimization of a robot’s physical design from that of its computational reasoning negatively affects the optimality of the overall system. Second, the requirement that the designers be experts inherently limits accessibility at a time when the proliferation of low-cost fabrication methods (e.g., 3D printing) has otherwise lowered barriers.

An ongoing research focus of our group is to develop co-optimization algorithms that automate and improve upon this costly and laborious process by encompassing all aspects of the design of embodied (i.e., robotic) systems. The co-optimization algorithms we develop in this thesis aim to produce optimized systems by considering the physics of sensors, actuators, and the environment, fabrication constraints, and the distribution of scenarios relevant for a particular application. These algorithms improve the quality of embodied systems, reduce the barrier to entry to robot design, and allow designers to focus on what they want the system to accomplish and not how it should be accomplished.

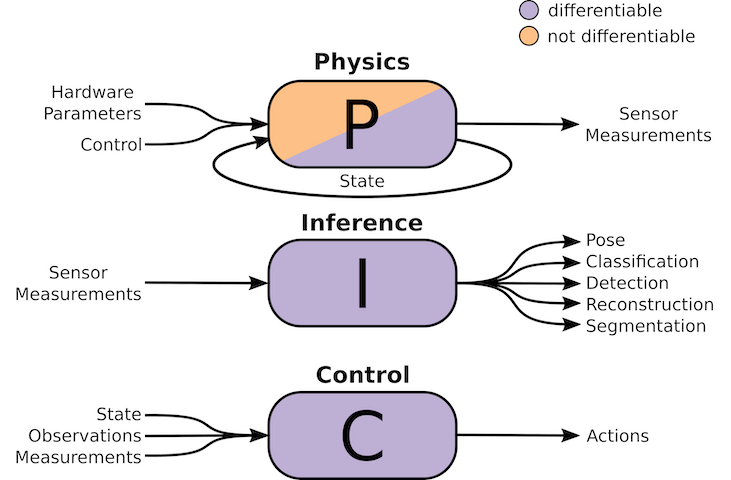
The ultimate goal for co-optimization algorithms in the context of robotics is to be able to optimize entire systems, including the physical design, sensors, inference, and control algorithms, in an end-to-end fashion based only on the definition of the task definition and (possibly) knowledge about the scenarios that the system is likely to encounter. In order to enable end-to-end optimization, a central theme in our work is to view an embodied system and its environment as a unified computational graph that considers physical parameters, physics, inference, and control as a cascade of operations for which the parameters can be optimized in an end-to-end fashion. Depending on the problem instance, physics, inference, and control blocks with varying structure can be stitched together to model the environment and the processes by which the desired task will be solved. This view encourages the end-to-end optimization of embodied systems directly for task objectives. Depending on the differentiability of the physics model used with respect to hardware parameters—which may or may not be a reasonable assumption based on the task at hand—all parameters of the system can be optimized end-to-end with deep learning techniques, or multiple optimization problems can be carried out simultaneously.

Optimizing Sensor Design and Inference for Beacon-based Localization

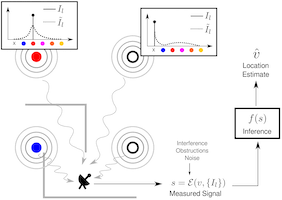
We have investigated the problem of joint optimization in the context of sensor network design, which involves reasoning over the distribution of a potentially diverse set of sensors in an environment together with a means of estimating certain spatial phenomena (e.g., temperature) from the noisy measurements that they provide. One such example is localization, which is critical for human and robot navigation, resource discovery, asset tracking, logistical operations, and resource allocation. In settings where GPS is not available (i.e., indoors, underground, or underwater), measurements from a fixed array of beacons provide an attractive alternative. Designing a system for beacon-based localization requires simultaneously deciding (a) how the beacons should be distributed (e.g., spatially and across transmission channels); and (b) how location should be determined based on measurements of signals received from these beacons. Note that these decisions are inherently coupled. The placement of beacons and their channel allocation influence the nature of the ambiguity in measurements at different locations, and therefore which inference strategy is optimal. Therefore, one should ideally search over the space of both beacon allocation—which includes the number of beacons, and their placement and channel assignment—and inference strategies to find a pair that is jointly optimal.

We developed a new learning-based approach to designing the beacon distribution (across space and channels) and inference algorithm jointly for the task of localization based on raw signal transmissions (Schaff et al., 2017). We instantiate the inference model as a neural network and encode beacon allocation as a differentiable neural layer that readily interfaces with this network. This unified architecture has the key advantage that allows us to use stochastic gradient descent, a standard technique for training neural networks, to jointly reason over the beacon allocation and inference parameters that are optimal for (robot) localization.

We evaluated our joint optimization framework under a variety of conditions related to the deployment of sensor networks—with different environment layouts, different signal propagation parameters, different numbers of transmission channels, and different desired trade-offs against the number of beacons. In all cases, we find that our approach automatically discovers designs—-each different and adapted to its environment and settings—that enable high localization accuracy. Comparisons to expert-designed baselines demonstrate that our method provides a way to consistently create optimized location-awareness systems for arbitrary environments and signal types, without expert supervision.

Optimizing Design and Control for Legged Locomotion

A robot’s ability to successfully interact with its environment depends both on its physical design as well as its proficiency at control, which are inherently coupled. Therefore, designing a robot requires reasoning both over the mechanical elements that make up its physical structure and the control algorithm that regulates its motion.

The problem of automating this co-optimization (design) process has a long history in robotics research. Much of the work in this area requires full knowledge of the dynamics of the system, and are restricted to settings with simple dynamics and must be initialized with high quality designs and controllers (or motion), which typically requires some level of domain expertise. More flexible approaches, which require no knowledge of the dynamics, employ evolutionary methods to optimize both design and control, but they suffer from high sample complexity and tend to yield poor design-control pairs.

Data-driven and learning-based methods, such as deep reinforcement learning, have proven effective at designing control policies for an increasing number of tasks. However, unlike the above methods, most learning-based approaches do not admit straightforward analyses of the effect of changes to the physical design on the training process or the performance of their policies—indeed, learning-based methods may arrive at entirely different control strategies for different designs. Thus, the only way to evaluate the quality of different physical designs is by training a controller for each—essentially treating the physical design as a “hyper-parameter” for optimization. However, training controllers for most applications of even reasonable complexity is time-consuming. This makes it computationally infeasible to evaluate a diverse set of designs in order to determine which is optimal, even with sophisticated methods like Bayesian optimization to inform the set of designs to explore.

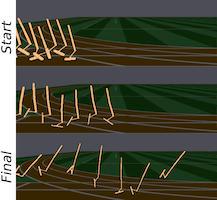
Continuing on our work on joint optimization, we developed an efficient algorithm that jointly optimizes over both a robot’s physical design and its corresponding controller (Schaff et al., 2019). Our approach maintains a distribution over designs and uses reinforcement learning to optimize a neural network control policy to maximize expected reward over the design distribution. Key to our approach is its proposed use of a single unified control policy that has access to a robot’s design parameters, allowing it to tailor its policy to each design in the distribution. Throughout training, we shift the distribution towards higher performing designs and continue to train the controller to track the design distribution through an approach analogous to multi-task reinforcement learning. In this way, our approach converges to a design and control policy that are jointly optimal. The figure above visualizes this refinement of the design and control policy (gait) during training (from “start” to “final”) for robots with different degrees-of-freedom. Our framework is applicable to arbitrary, but fixed, robot morphologies, tasks, and environments. We evaluate our method in the context of legged locomotion, parameterizing the (continuous) length and radius of links for several different robot morphologies. Experimental results show that starting from random initializations, our approach consistently finds novel designs and gaits that exceed the performance of manually designed agents and state-of-the-art optimization baselines, across different morphologies and environments.

A limitation of this algorithm is that it requires that the morphology be predefined and focuses instead on optimizing the continuous design parameters associated with that morphology. We subsequently extended our framework to remove the need for the user to specify the morphology. The result is an algorithm that is able to optimize over any number of kinematic or dynamic design parameters such as the number and arrangement of limbs or the position and type of the controllable degrees of freedom. However, the search over discrete morphologies and their controllers significantly complicates the approach described above. First, it introduces a search over a prohibitively large, discrete, and combinatorial space of morphologies. Second, the state and action spaces can vary across morphologies, making the multi-task reinforcement learning problem more complicated and the design-conditioned control policy challenging to implement.

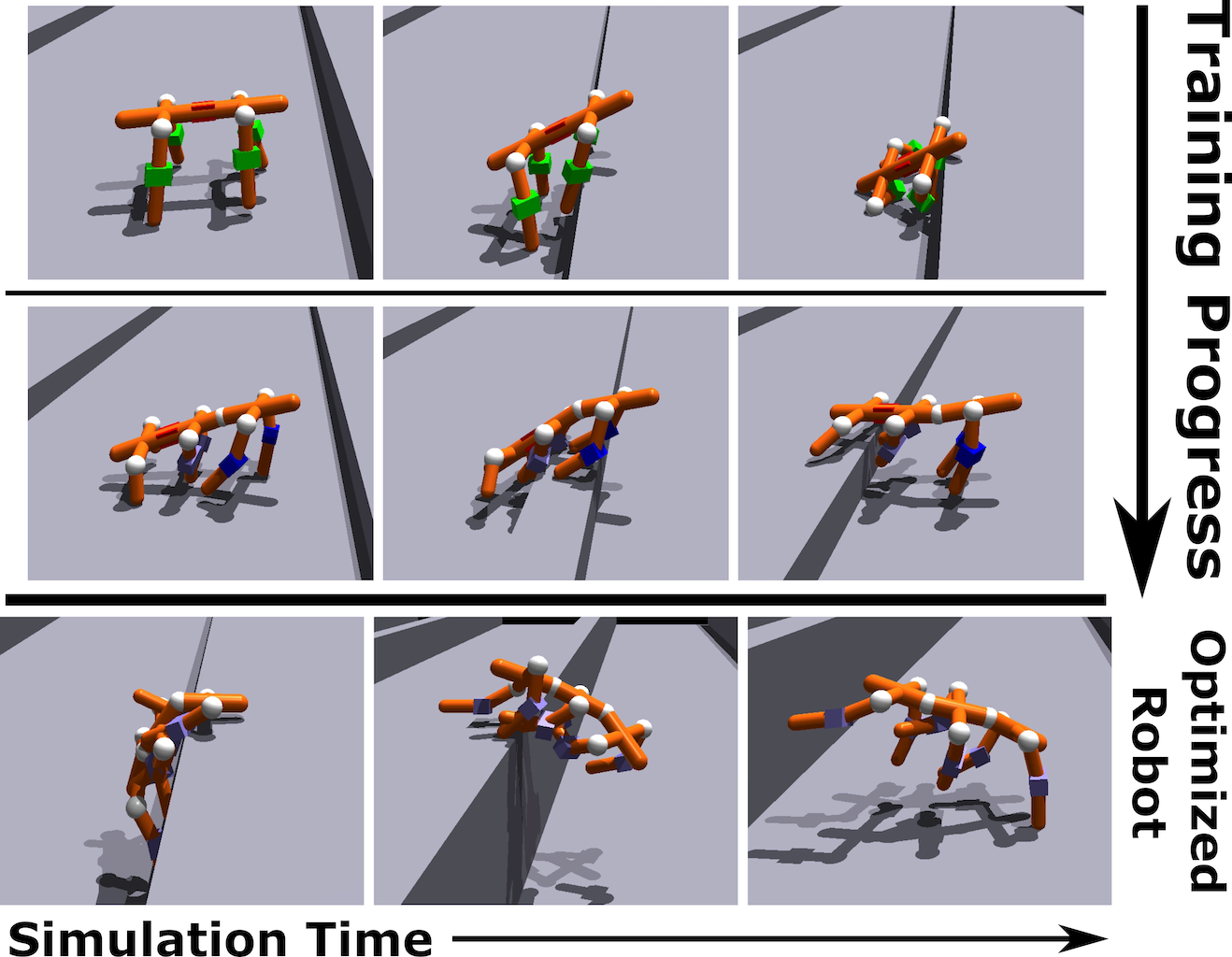
We proposed Neural Limb Optimization (Schaff & Walter, 2022) to overcome these challenges to allow for joint optimization over the set of robot morphologies and the parameters of a unified controller through three key contributions. First, represents the space of morphologies with a context-free graph grammar. This has two benefits: it allows for the easy incorporation of fabrication constraints and inductive biases into the optimization through the symbols and expansion rules of the grammar; and it provides a way to iteratively generate designs simply by sampling expansion rules. Second, the grammar allows us to define complex, multi-modal distributions over the space of morphologies via a novel autoregressive model that recursively applies expansion rules of the grammar until a complete graph has been formed. Third, we develop a morphologically-aware transformer architecture to parameterize the design-conditioned control policy. The flexible nature of transformers allows the model to easily adapt to changes in the state and action spaces of different morphologies. For more details, see our paper below (Schaff & Walter, 2022).

Optimizing Design and Control for Soft Crawling Robots

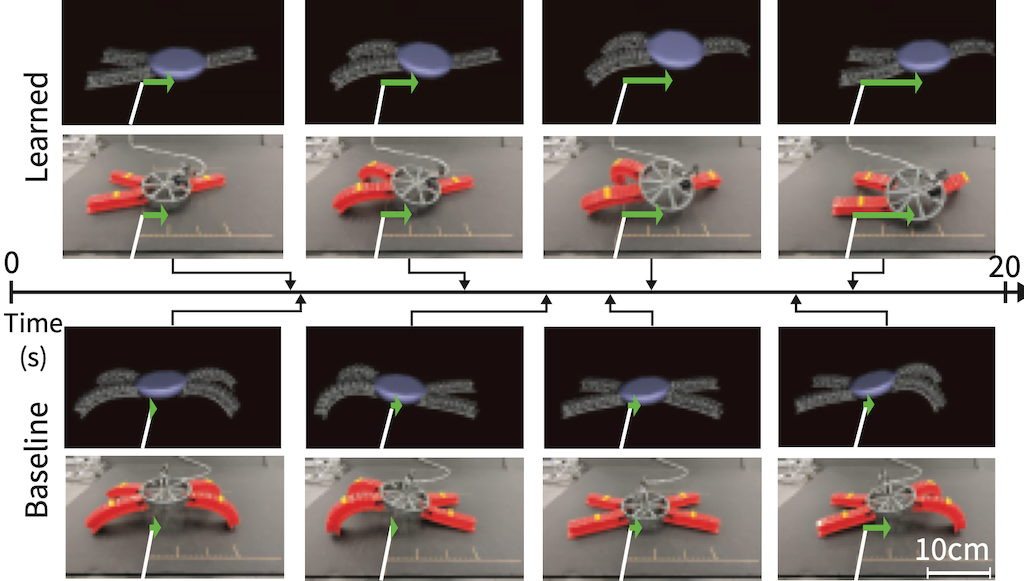
The aforementioned work on optimizing the design and control of legged robots was only evaluated in simulation. While existing work suggests the ability for legged robot controllers trained in simulation to transfer to the real world, it was not clear whether the same would be true of sim-to-real transfer of the designs. In an effort to better understand the capacity for our learned design-control pairs to transfer, we investigated an extension of our architecture to the problem of developing crawling soft robots. Compared to their rigid-body counterparts, soft robots exhibit characteristics that make them both interesting targets for joint optimization and amenable to studying sim-to-real transfer. First, the deformable nature of soft robots enables designs that respond to contact or control inputs in sophisticated ways, with behaviors that have proven effective across a variety of domains. This property tightly couples design and control, and “good” designs will allow for control algorithms that exploit the deformability of the robot in useful ways. Second, the type of soft robots that we considered (pneumatically actuated silicone bodies) can be easily fabricated, requiring only a 3D-printed mold, low-cost material (silicone), and off-the-shelf pressure regulators. Together, these characteristics make soft robotics a natural choice for the co-optimization of design and control.

However, the high-fidelity simulation of soft robots remains an open problem. Deformable material simulators are often computationally intensive with wall-clock times that are orders-of-magnitude larger than those used to simulate rigid-bodied robot. It is challenging to create a simulator that is both accurate enough to allow for sim-to-real transfer and fast enough to sufficiently explore the joint design-control space. Several simulation techniques have been proposed in recent years that trade off between speed and physical accuracy. However, recent co-optimization methods for soft robots rely on faster simulations, at the expense of accuracy, and rarely attempt to transfer their optimized robots from simulation to reality.

We proposed a complete framework for the simulation, co-optimization, and sim-to-real transfer of the design and control of soft legged robots (Schaff et al., 2022). In our approach, we propose a design-reconfigurable model order reduction technique that enables fast and accurate finite element simulation (FEA) across a large space of physical robot morphologies. FEA is the defacto standard for simulating deformable materials with a high degree of accuracy. Using this design-reconfigurable model order reduction method, we extend our previous work on co-optimization of design and control with a deep multi-task reinforcement learning policy to optimize over a discrete set of designs. We build optimized, pneumatically actuated soft robots and transfer their learned controllers directly to reality, without any fine-tuning on the real robot. Experiments reveal that our method produces systems that outperform a standard expert-designed crawling robot in the real world.

References